dom
01
jun
2014
La electricidad - Tecnología
La electricidad está formada por millones de electrones. Se genera una corriente eléctrica cuando éstos se desplazan. Un ejemplo es la electricidad estática, que produce que al frotar por ejemplo un bolígrafo contra un jersey, el primero adquiere una pequeña carga eléctrica y pueda atraer pequeños trozos de papel. Pero esta energía tiene tan poca potencia que no tiene apenas utilidad. La electricidad se produce en centrales eléctricas de diferentes tipos, para después ser transportada por los tendidos eléctricos hasta los lugares de consumo. En las centrales térmicas se usa un alternador que gira gracias a una fuerza (en el caso de las centrales térmicas, el vapor de agua generado al quemar carbón; en el caso de las centrales eólicas, la fuerza del viento; etc.) Este alternador se basa en los efectos electromagnéticos de la corriente eléctricas: cuando un conductor se mueve dentro de un campo magnético, se genera electricidad. Se puede observar un esquema de un alternador en el siguiente gráfico:

Un circuito eléctrico es un circuito cerrado a través del cual pasa la electricidad, proporcionando energía a los diferentes elementos para que funcionen. En el momento en que el circuito deje de ser cerrado (porque se rompa el cable, porque se estropee una bombilla y no pase la electricidad o por diferentes causas) deja de pasar la electricidad y no funciona. Ejemplo de circuito eléctrico:

|

|
|
Esquema de un circuito eléctrico |
El mismo circuito eléctrico, con objetos reales |
PARTES DE UN CIRCUITO ELÉCTRICO
Todos los circuitos eléctricos se componen de varios elementos (puede haber varios de cada):
|
GENERADORES |
CONDUCTORES |
RECEPTORES |
ELEMENTOS DE CONTROL |
|
Proporcionan la electricidad al circuito.
Pilas y baterías. |
Transportan la electricidad por todo el circuito Ejemplo y símbolo: Cables: |
Son los motores que transforman la electricidad que reciben. Ejemplos y símbolos: · A sonido: · A movimiento: · A calor: / · A luz: |
Activan o desactivan el circuito abriéndolo o cerrándolo. Ejemplos y símbolos: · Interruptor: · Pulsador: · Conmutador: |
(aunque podría no haber elementos de control, no sería práctico, porque no se podría apagar)
INTENSIDAD, RESISTENCIA Y VOLTAJE EN UN CIRCUITO. LEY DE OHM
Los circuitos eléctricos, para funcionar, deben tienen siempre:
- Intensidad: es el número de electrones que pasan por los cables. Se mide en Amperios (A).
- Resistencia: es la resistencia que opone un material a que pasen los electrones por él. Se mide en Ohmios (Ω).
- Voltaje: es la intensidad con la que envía los electrones la pila. Se mide en Voltios (V).
Para hallar un dato que nos falte de esos tres, utilizamos la siguiente fórmula (la Ley de Ohm):
V = I · R
Aunque a partir de ella podemos derivar las siguientes dos, depende de qué datos tengamos (¡ATENCIÓN! El símbolo "·" es un signo de multiplicación):
R = V : I
I = V : R
En éstas fórmulas, V es el voltaje; I, la intensidad; y R, la resistencia. Pero también tenemos que tener en cuenta que la disposición de los receptores del circuito:
|
SERIE |
PARALELO |
|
Todos los receptores están en el mismo cable, y solo hay un camino diferente para que pase la electricidad. Ejemplo:
|
Los receptores están en cables diferentes, de manera que hay dos o más caminos diferentes para que pase la electricidad. Ejemplo:
|
Así pues, para hallar la resistencia total no seguimos el mismo procedimiento. Estos serían los procedimientos:
|
SERIE |
PARALELO |
|
Para hallar la Resistencia Total (Rt) simplemente sumamos todas las resistencias. En este caso sería así: Rt = R1 + R2 = 3 + 5 = 8 Ω Si hubiera tres o más resistencias, las sumaríamos todas. |
Aquí no utilizaremos el mismo procedimiento, porque los electrones escogen el camino más fácil, así que la mayoría escogerán el que menos resistencia tenga (en este caso el superior). La fórmula es la siguiente: Rt = (R1 · R2) : (R1 + R2) En este caso, la fórmula la haríamos así: Rt = (3 · 5) : (3 + 5) = 15 : 8 = 1,875 Ω Si hubiese tres o más caminos la fórmula sería algo más compleja; aquí, no la vamos a ver. |
El dato que acabamos de hallar con estas fórmulas será el que debamos incluir en la fórmula V = I · R
jue
24
abr
2014
Las poleas con correa
Los engranajes son ruedas con "picos" que engranan unos con otros, transmitiendo la fuerza. Giran en direcciones contrarias. Puedes observarlo en las animaciones de la parte inferior de esta página. Son reversibles, pues giremos la primera rueda o la segunda, transmite el movimiento a la otra rueda.
Tenemos los siguientes datos de los engranajes:
- n1: Velocidad en RPM (Revoluciones Por Minuto) de la rueda 1
- z1: Número de dientes de la rueda 1
- n2: Velocidad en RPM (Revoluciones Por Minuto) de la rueda 2
- z2: Número de dientes de la rueda 2
Para averiguar un dato que nos falte de estos anteriores, usaremos la siguiente fórmula:
z1 · n1 = z2 · n2
Para resolverlo, sustituimos los datos que sepamos y el que nos quede lo dejamos tal cual (por ejemplo, 9 · n1 = 3 · 6).
Para resolver esto, multiplicamos los datos del lado que tenga los dos datos y los dividimos entre el dato que nos queda en el otro lado del signo [ = ]. Así nos quedaría (3 · 6) : 9 = 18 : 9 = 2
Click para mostrar u ocultar la operación completa
Para evitar confusiones, aclaro que [ · ] es el signo de multiplicación [ x ].
Hay varios tipos de engranajes: de velocidad constante, de velocidad multiplicadora y de velocidad reductora. Abajo explico todos de forma detallada, e incluyendo unas animaciones.
Poleas con correa de velocidad constante
Los engranajes de velocidad constante son los dos del mismo tamaño, por lo que el número de vueltas es igual para los dos engranajes (es decir, i = 1).
Puedes observarlo en la animación de la derecha.
Poleas con correa de velocidad multiplicadora
Los engranajes de velocidad multiplicadora no son del mismo tamaño. El primer engranaje es mayor, por lo que el número de vueltas es mayor en el segundo engranaje (es decir, i > 1).
Puedes observarlo en la animación de la derecha. Fíjate en que cuando la rueda pequeña ha dado una vuelta completa, la rueda grande casi no ha avanzado.
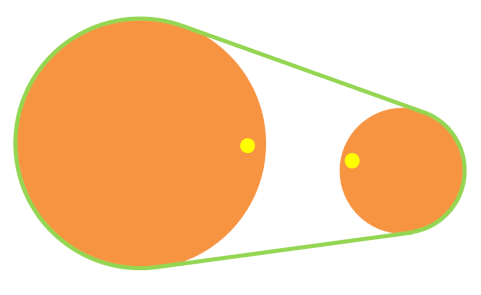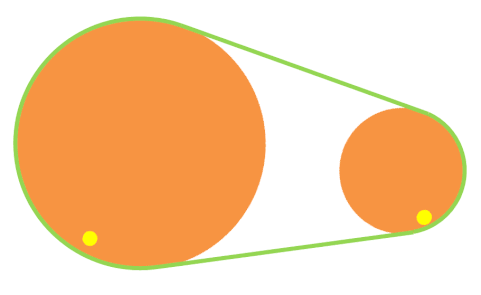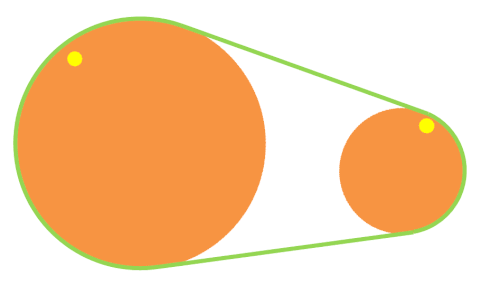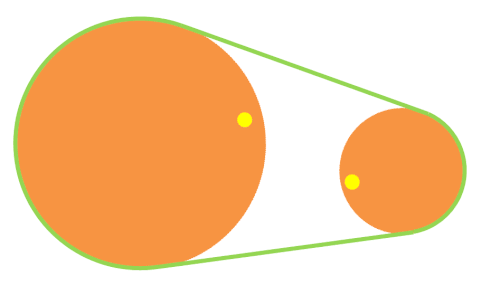
Poleas con correa de velocidad reductora
Las poleas con correa de velocidad reductora son de tamaños diferentes. La segunda poleas con correa es mayor, por lo que el número de vueltas es menor en la segunda poleas con correa (es decir, i < 1).
Puedes observarlo en la animación de la derecha. Fíjate en que cuando la rueda pequeña ha dado una vuelta completa, la rueda grande casi no ha avanzado.
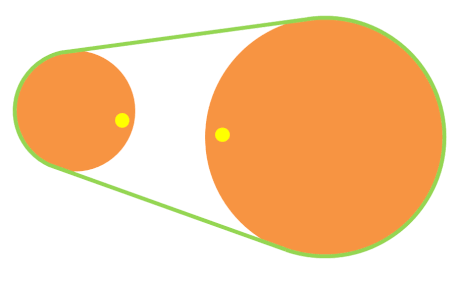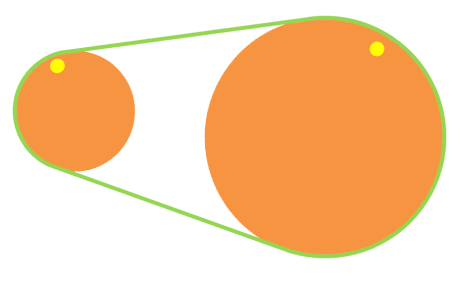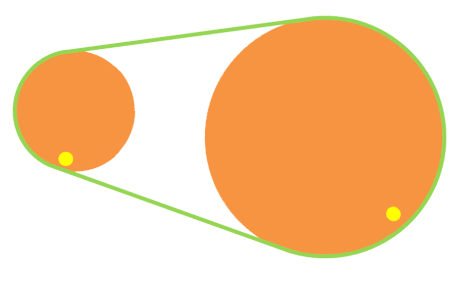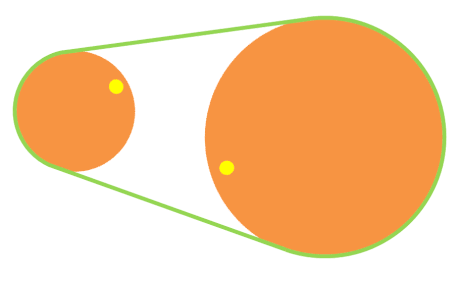
Para saber cuántas vueltas da la segunda rueda por cada vuelta que da la primera, usamos una de las siguientes fórmulas:
i = n2 : n1 / i = z1 : z2
Las dos fórmulas dan el mismo resultado. Al número de vueltas que da la segunda rueda por cada vuelta que da la primera se le llama relación de transmisión.
A continuación, si hacéis clic en los correspondientes títulos, podréis ver ejemplos cómo resolverlas:
Click para mostrar u ocultar la solución con la primera fórmula |
Click para mostrar u ocultar la solución con la segunda fórmula |
En este caso, los dos ejemplos son de velocidad multiplicadora
mié
23
abr
2014
Las poleas y los polipastos
LA POLEA Y EL POLIPASTO
Las poleas son ruedas con una hendidura en el centro por la que pasa una cuerda o correa. Se utiliza para elevar objetos. Con una polea simple no proporcionamos ventaja mecánica (hay que hacer la misma fuerza que la que hace el objeto), pero se aumenta la comodidad (pues es más cómodo tirar desde arriba hacia abajo que desde abajo hacia arriba). También hay poleas compuestas, llamadas polipastos, con los que se puede reducir el esfuerzo necesario. A continuación vemos ejemplos de los tipos de poleas con algunas animaciones:
POLEAS SIMPLES
No nos proporcionan ventaja mecánica, pero nos facilitan el trabajo, pues es más cómodo estirar hacia abajo que hacia arriba.

En las poleas simples, la fuerza debe ser igual a la que ejerce el objeto que deseamos levantar (la resistencia).
F = R
POLIPASTOS
Además de comodidad, nos proporcionan ventaja mecánica. Esta ventaja varía según el número de poleas. Para calcularla, dividimos el peso del objeto que queremos elevar entre el número de poleas. La rueda que se mueve se denomina "rueda móvil".
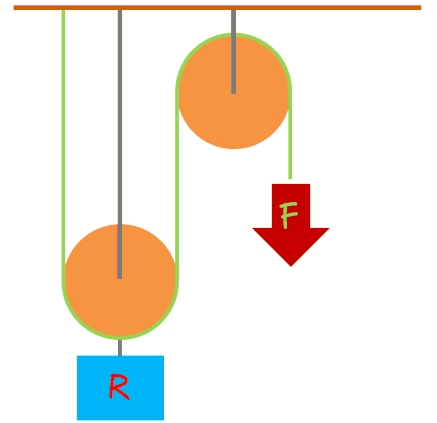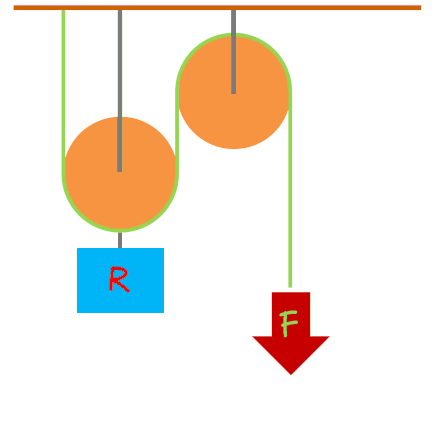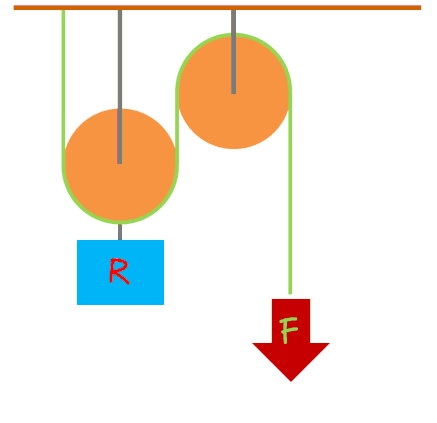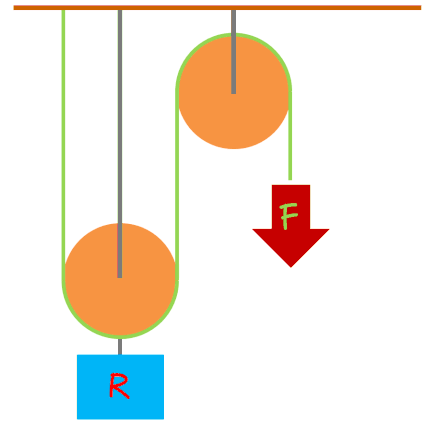
En los polipastos, la fuerza debe la resistencia dividida entre el número de ruedas.
F = R : nº ruedas
VARIANTES DE LA POLEA
POLEAS CON CORREA | RUEDAS DE FRICCIÓN
(ver artículo individual) | (ver artículo individual)
sáb
12
abr
2014
Los engranajes
Los engranajes son ruedas con "picos" que engranan unos con otros, transmitiendo la fuerza. Giran en direcciones contrarias. Puedes observarlo en las animaciones de la parte inferior de esta página. Son reversibles, pues giremos la primera rueda o la segunda, transmite el movimiento a la otra rueda.
Tenemos los siguientes datos de los engranajes:
- n1: Velocidad en RPM (Revoluciones Por Minuto) de la rueda 1
- z1: Número de dientes de la rueda 1
- n2: Velocidad en RPM (Revoluciones Por Minuto) de la rueda 2
- z2: Número de dientes de la rueda 2
Para averiguar un dato que nos falte de estos anteriores, usaremos la siguiente fórmula:
z1 · n1 = z2 · n2
Para resolverlo, sustituimos los datos que sepamos y el que nos quede lo dejamos tal cual (por ejemplo, 9 · n1 = 3 · 6).
Para resolver esto, multiplicamos los datos del lado que tenga los dos datos y los dividimos entre el dato que nos queda en el otro lado del signo [ = ]. Así nos quedaría (3 · 6) : 9 = 18 : 9 = 2
Click para mostrar u ocultar la operación completa

Para evitar confusiones, aclaro que [ · ] es el signo de multiplicación [ x ].
Hay varios tipos de engranajes: de velocidad constante, de velocidad multiplicadora y de velocidad reductora. Abajo explico todos de forma detallada, e incluyendo unas animaciones.
Engranajes de velocidad constante
Los engranajes de velocidad constante son los dos del mismo tamaño, por lo que el número de vueltas es igual para los dos engranajes (es decir, i = 1).
Puedes observarlo en la animación de la derecha.

Engranajes de velocidad multiplicadora
Los engranajes de velocidad multiplicadora no son del mismo tamaño. El primer engranaje es mayor, por lo que el número de vueltas es mayor en el segundo engranaje (es decir, i > 1).
Puedes observarlo en la animación de la derecha. Fíjate en que cuando la rueda pequeña ha dado una vuelta completa, la rueda grande casi no ha avanzado.

Engranajes de velocidad reductora
Los engranajes de velocidad reductora no son del mismo tamaño. El segundo engranaje es mayor, por lo que el número de vueltas es menor en el segundo engranaje (es decir, i < 1).
Puedes observarlo en la animación de la derecha. Fíjate en que cuando la rueda pequeña ha dado una vuelta completa, la rueda grande casi no ha avanzado.

Para saber cuántas vueltas da la segunda rueda por cada vuelta que da la primera, usamos una de las siguientes fórmulas:
i = n2 : n1 / i = z1 : z2
Las dos fórmulas dan el mismo resultado. Al número de vueltas que da la segunda rueda por cada vuelta que da la primera se le llama relación de transmisión.
A continuación, si hacéis clic en los correspondientes títulos, podréis ver ejemplos cómo resolverlas:
Click para mostrar u ocultar la solución con la primera fórmula |
Click para mostrar u ocultar la solución con la segunda fórmula |
En este caso, los dos ejemplos son de velocidad multiplicadora
jue
30
ene
2014
Ejercicios interactivos de estructuras - autocorregibles
|
El cable de una grúa. Tracción. Compresión. Flexión. Cizalladura. Torsión. |
El trampolín, en su extremo fijo : Tracción. Compresión. Flexión. Cizalladura. Torsión. |
|
Estando de pie, el fémur (hueso de la pierna): Tracción. Compresión. Flexión. Cizalladura. Torsión. |
Un piñón de la bicicleta: Tracción. Compresión. Flexión. Cizalladura. Torsión. |
|
Cimientos de un edificio: Tracción. Compresión. Flexión. Cizalladura. Torsión. |
Viga de una casa: Tracción. Compresión. Flexión. Cizalladura Torsión. |
|
Una llave mientras abrimos con ella una puerta: Tracción. Compresión. Flexión. Cizalladura. Torsión |
Una alcayata de la que cuelga un cuadro: Tracción. Compresión. Flexión. Cizalladura. Torsión. |
|
Una columna de una iglesia: Tracción. Compresión. Flexión. Cizalladura. Torsión. |
Un tornillo mientras se está atornillando: Tracción. Compresión. Flexión. Cizalladura. Torsión. |
|
Estando de pie y con los brazos caídos, el radio (hueso del brazo): Tracción. Compresión. Flexión. Cizalladura. Torsión. |
La barra en la que hacen ejercicios los gimnastas: Tracción. Compresión. Flexión. Cizalladura. Torsión. |
Elaborados por Antonio González García y Javier Zamora Martín, profesores del IES Al Iscar
jue
14
nov
2013
LOS METALES: resumen y ejercicios
Los ejercicios están en "AVERIGUA LO QUE SABES"
mar
12
nov
2013
LA MADERA Y EL PAPEL
Originalmente hecho por Andrea Villanúa, compañera mía. Mis agradecimientos.
|
Menú de Navegación |
|
Suscríbete a nuestro Boletín de noticias. Recibirás actualizaciones de la página, promociones y mucho más. No somos pesados ni mandamos spam. No proporcionaremos tu e-mail a terceros. |
|
Sidebar Foto de fondo: pixabay.com La página puede cambiar dependiendo de tu resolución de pantalla.  by DMRights by DMRights
CreativeCommons  ACTINTERACTIVA-2º ESO, de Jorge Bruned, ACTINTERACTIVA-2º ESO, de Jorge Bruned,tiene una licencia Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Unported License. Contador de Visitas Contador en marcha desde el 09/09/2013
Buscador:
|
